How to Handle Hidden Exponentials

Where exponential growth can lurk and why its potential existence should shift our thinking from probabilities to possibilities

If you have a sense of what the future could look like, you can make decisions today to bend tomorrow towards benevolence. When it comes to investing, government planning, research funding, personal life, and more, we make decisions based on hard and fast rules, stochastic processes, and the unknown. While it is possible to reason about how to deal with the laws of physics and make predictions about probabilistic phenomena, the playbook for handling uncertainty requires a bit more intuition. When it comes to immeasurable unknowns, what is probable needs to redefined and reconsidered as what is possible. This is especially true when you suspect an unknown is driven by exponential growth.

Starting with a simple hypothetical casino game, this essay explores how an exponential distribution can lurk behind what appears to be a profitable looking gamble. What looks like a good series of bets in theory can turn out to be quite dangerous in the real world. The difference between additive and multiplicative growth rates changes the nature of decision making. Multiplicative growth rates can create probability spaces that grow faster than they can be explored in time, which makes a system prone to ruin. In the blinding light of uncertainty, the precautionary principle - a refocusing of cost-benefit calculus to survival preparation - is a necessary and courageous heuristic to apply to a class of rare phenomena with deadly consequences that tend to be driven by hidden exponentials. Some of these phenomena include epidemics, terrorism, and climate change. We will consider the ongoing coronavirus pandemic and why we should treat novel viruses (especially fast spreading ones that can kill people) very differently than the flu. When we identify potential hidden exponentials, we can make choices that limit our downside. Sometimes, we can even make choices that offer unlimited upside.

In the real world, expected value can be less than expected

How do you make decisions in an uncertain world? It depends. If you can quantify your uncertainty, then decision making boils down to weighing tradeoffs between benefits and costs. This pragmatic tradeoff considering all potential outcomes and their likelihoods can be represented as expected value under the law of large numbers. 

Now, let’s imagine that we arrive at a casino on its opening night, and we sit down to play a simple game based on flipping a coin. The rules are simple. You can bet whatever you want. If the coin comes up heads, then you get your bet back plus another 50%. If the coin comes up tails, then you get back only 60% of your bet. 

Would you want to play this game? Given that heads and tails are equally likely outcomes, you gain more when the coin comes up heads than you lose when the coin comes up tails, and you can bet whatever you want, this could be a really profitable game. We can project how profitable a single bet will be by calculating its expected value, which is the mean of the probability distribution. Here, it is 105% of the bet. In simple mathematical notation, the game can be represented with probability distribution F(x) and expected value E(x).  

Now, let’s imagine a friend of ours, let’s call him Robert, joins us at the table. He laughs at the odds and boasts that he can put the casino out of business on its opening night by betting his $100,000 of life savings. We know Robert to be a bit overconfident and have a naïve understanding of probability. Nonetheless, we are curious about what is sure to be a costly lesson for him and a free lesson for us. Robert explains that the expected value of the game is 105% of whatever one bets, which means that the maximum expected value of playing the game n times is 1.05 to nth power multiplied by one’s entire budget. He does the math in his head and explains that $100k times 1.05 to the 200 is 1.7 billion dollars. All he needs to do is play about 200 rounds to become a billionaire and wipe out the casino. 

It might not surprise you that something is off with Robert’s strategy. Most people have an intuitive understanding that one should never bet what one cannot afford to lose. Not Robert. His strategy is to bet his entire net worth each round. Unfortunately, he is missing equal parts humility, intuition, and an understanding of probability. From a probability perspective, Robert fails to grasp the finite nature of the real-world and the uneven distribution of payoffs across possible trajectories. Take a look at the payout pyramid below. After five rounds of betting his entire budget, Robert has a positive expected value but faces a 69% chance of losing money. What do you expect will happen as he plays more rounds?

As Robert plays more and more rounds, his expected value continues to increase and his likelihood of losing almost everything also increases. If he makes a profit, he could make a huge profit, but more likely, he will lose his money. Below is a graph showing a random sample of 1,000 trajectories (simulated via a Monte Carlo process) across 1,000 iterations of the game. In this simulation, there is only a single trajectory showing a positive return on investment. In most other simulations of 1,000 trajectories, there is not a single trajectory showing a positive return. If this was the real world, Robert would likely have to leave the casino with only a fraction of a penny to his name. 

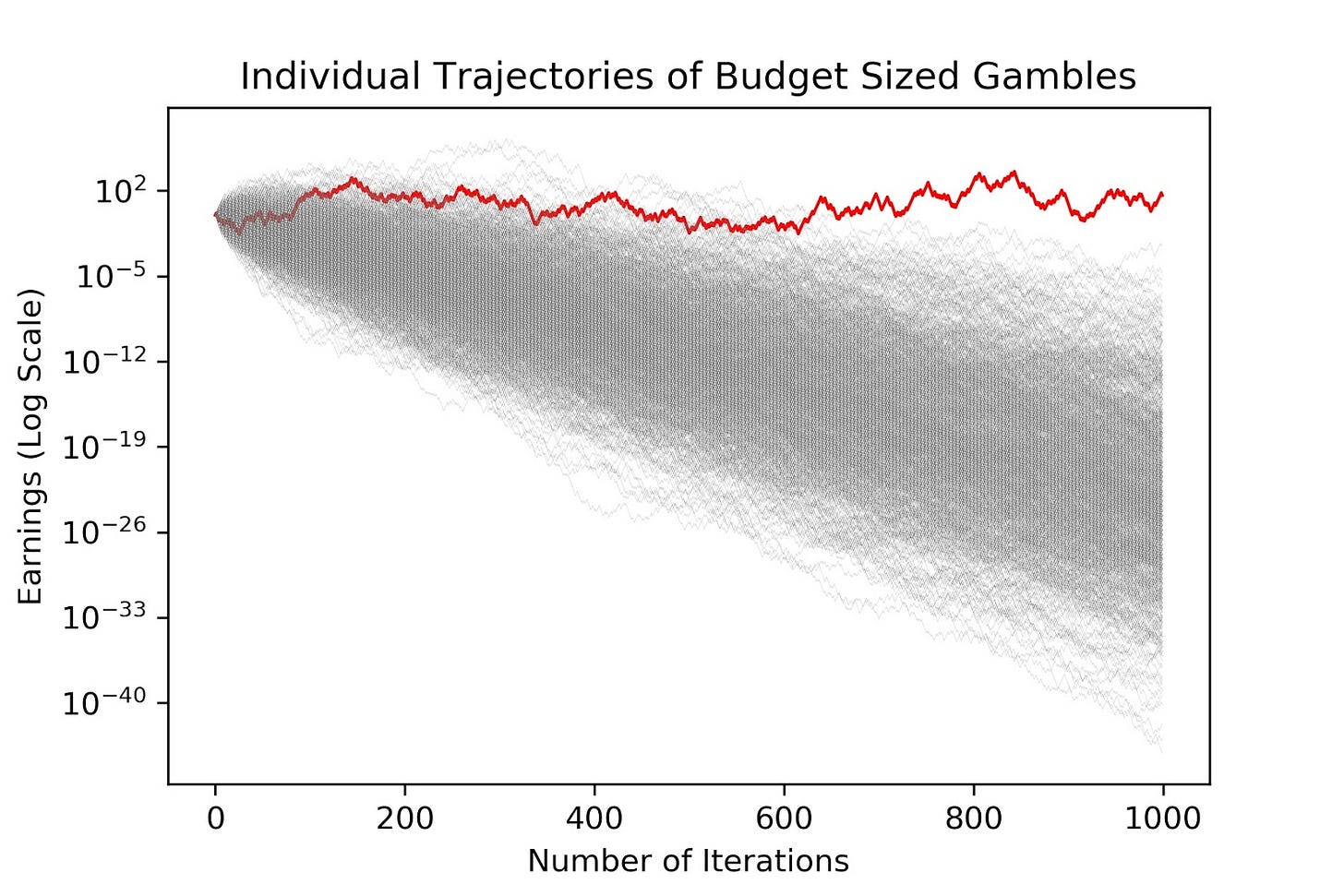
The consecutive budget sized gambles affect the higher level moments of the probability distribution function such that the mean of the distribution approaches infinite while the median approaches zero. Recall from statistics that the mean is the sum of the values divided by the number of values and the median is the midpoint of a distribution. By the 200th round, this shifted distribution means that there is now a few in a billion chance of making an ungodly sum of money and a really huge chance of losing everything.

When Robert bets his entire budget rather than a fixed amount, he is transforming what could be a normal distribution of payoffs (when betting a fixed amount) into an exponential distribution of payoffs. The expected value of a series of fixed value gambles is less than the budget sized gambles, but the likelihood of profiting is much higher. Below is a graph of a random sample of 1,000 trajectories over 1,000 rounds of the same game where you bet a fixed amount, say $1, every round. This choice of fixed size gambles makes it impossible to earn a sextillion within 1,000 rounds (a sextillion is 10^21 and comes from 1.05^1000), but a fixed size gamble nearly ensures that you make at least 300 times your fixed amount. 

The high-level lesson here is that you should never bet what you cannot afford to lose. The more technical lesson is that time-series averages (represented by individual trajectories) may look different than ensemble averages (the expected value) when the game can only be played a finite number of rounds. If you’re curious about how to plot these, check out the code to reproduce these plots at the end of the post. And, for what it is worth, neither a fixed bet nor budget sized bets are the optimal strategy for such a game. If you’re curious about how to formulate the optimal bet, you should check out the Kelly Criteria, which is based on betting a fraction of one’s budget.    

This particular example and insight into how time-series averages differ from ensemble averages has been explained by Nassim Taleb in Incerto and is explained in a recent paper published by Ole Peters titled The ergodicity problem in economics. Ergodicity simply refers to stochastic processes where the time-series average is equivalent to the ensemble average. When a system is ergodic, we can confidently optimize the expected value. When we know not if a system is ergodic, we should be wary of ruin. 

Probabilities versus possibilities

If we were to write the laws of decision-making, then we might borrow some style from Isaac Asimov’s three laws of robotics. The laws of decision-making under uncertainty are as follows: First, avoid the possibility of ruin. Second, apply qualitative heuristics to consider what is plausible. Third, quantify the probabilities. The order matters.

The flu versus the novel virus

Before getting into thinking about the flu vs. a novel virus, let’s take stock of what we know is going on with coronavirus. Today is March 18th, 2020. Based on data from the WHO compiled by Our World in Data, there have been 179,112 confirmed cases of coronavirus and 7,426 confirmed deaths globally. All of Italy and France are on lockdown. The Bay Area ordered residents to shelter in place. Schools in Boston are closed. Universities across the United States sent students home. The S&P 500 has dropped over 25% since January 1st. While the coronavirus originated in China and China has the most confirmed cases (81,116), China has reduced the spread of the virus dramatically. It has been over a month since China’s confirmed cases have doubled. 

In the two figures below, I plot the confirmed cases of COVID-19 and the associated deaths as a proportion of a country’s population to show what we know about the current range of outcomes. What we do not know is to what degree the confirmed cases underestimate the actual cases or how much the death rate lags the infection rate. In the United States, the confirmed cases are most likely a vast underestimate of the actual cases given the lack of testing. The true number and rate of spread of the virus in the US is likely to look more like the European countries than the available data suggests. In order to save lives, we need to take action such that we “flatten the curve” (avoid overwhelming the health systems) and look more like China and South Korea. Everyone can help by washing their hands and social distancing. It may be possible for parts of the US to avoid what is happening in Europe and shift its trajectory to what is happening in China.

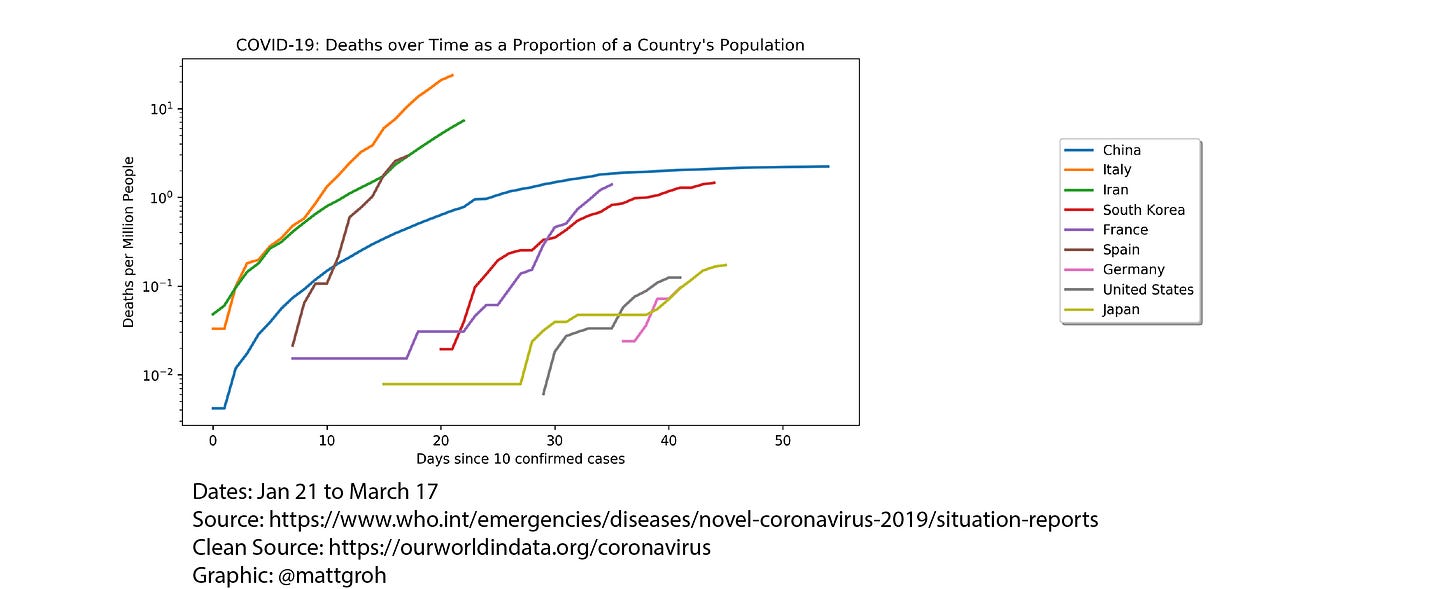
Now, most policy makers recognize that the coronavirus is very different than the flu and requires extraordinary action. But, when should policy makers, business executives, universities, and others have started paying attention? Why should we be wary of something we normally do not pay attention to that has a low likelihood of occurring? 

More specifically, why should we always treat novel viruses differently than the flu? The flu reoccurs every year, and the CDC estimates that this year the flu infected 45 million Americans and killed 46,000 people. The flu is something we know and rarely worry about. It is nice to not worry, and it is cognitively easy to lump a novel virus with the flu before we have lots of data. Novel viruses are by definition something new, and we do not immediately know how innocuous or bad they can be. In the case of coronavirus, confirmed cases in China doubled every two days in late January from 278 confirmed cases and 6 deaths on January 21st to 1985 confirmed cases and 56 deaths on January 26th.  

We specifically should not coarsely associate the novel coronavirus with the flu because of the underlying uncertainty, exponential growth rates, and potential consequences. First, we do not know much about the novel coronavirus. Second, since January we have known that there is an exponential growth rate at play. Moreover, the mortality rate, as estimated using data from January 21st to January 26th in China, is 200 times higher for the coronavirus than the flu. It is uncertain whether such data is representative, but if it is then we certainly want to address this. The failure to prepare for an epidemic can lead to a similar outcome as Robert’s budget sized gambles with a high positive expected value game in a non-ergodic probabilistic space.

On January 26, Joseph Norman, Yaneer Bar-Yam, and Nassim Taleb published a note titled Systemic risk of pandemic via novel pathogens – Coronavirus: A note outlining why to consider the precautionary principle when facing a risk of pandemic. In their note, the authors explain that “the precautionary principle should apply when traditional statistical averages are invalid because risks are not ergodic.” In other words, costs and benefits are the wrong thing to optimize for when there is a risk of ruin. We will survive this pandemic. But, if humanity does not deeply focus on survival each time it faces a potential pandemic, the probability of species-level survival will approach zero over the long run. 

Naturally, we want to avoid extinction. As a consequence, it is imperative to bend risks towards ergodicity by taking extraordinary measures like national lockdowns and shelter in place orders. These kinds of measures can be effective because (a) the basic reproduction rate of a pathogen is jointly determined by the pathogen and human behavior and (b) the mortality rate is jointly determined by the pathogen and availability of healthcare. If we successfully avoid a crisis, it may appear like we overreacted because we will never know how bad it could have been. But, if we learn how bad something can be, it might be too late to avoid its consequences.

When it comes to possibilities with hidden exponentials, we shift our thinking from the probable to the possible listening to our intuitive survival instinct. This leads to second and third order effects. For example, survival mode can create a lot of anxiety and uncertainty can induce feelings of helplessness. It may be hard to measure the impact of empathy, generosity, kindness, and care, but the practice of these values and their impact on the world may be driven by multiplicative growth. In addition to social distancing and hand washing, it is time to catch up with old friends and generously support our local communities. Positivity can grow exponentially too.

Infinite Affirmation

You may have heard that smiles are infectious. How can you not smile when you see a little kid riding his tricycle with a big old grin on his face? Did you know affirmations can be contagious and full of healing properties too? You don’t have to take my word for it, but I promise that listening to others and offering emotional support creates a virtuous cycle of positivity.

Sometimes problems cannot be simply solved. When there’s no outside fix, we have to learn how to embrace and live through challenges. That’s where social affirmations come in. Social affirmations are words or acts of care, kindness, generosity, and empathy. These words and acts do not directly fix the problem. But they offer solidarity, reassurance, and reflection. Affirmations remind us of the values that we hold most dear that we must continually practice.

Social affirmations have the potential to become infinite loops where one friend offers an affirmation, the other affirms the affirmation, the first then affirms the affirmation of the affirmation, and the process goes on as such. If you’re going to be stuck in a loop, the loop of affirmation is a pretty sweet spot to find yourself. And, find yourself you will. There’s infinite upside there.

---

If you enjoyed reading about decision making and hidden exponentials, then sign up below to get an email when the next ideas come out. And, please share your comments via email or in the comment section below. I’d love to learn from you.

---

p.s. Here’s the python script to reproduce the Monte Carlo simulations of budget-sized and fixed-sized gambles.

import random
import numpy as np
import matplotlib.pyplot as plt
trajectories = []
for examples in range(0,1000):
    budget = 1
    individual = [1]
    for steps in range(1,1000):
        if random.randint(0,1)==1:
            budget = budget*1.5
        else:
            budget = budget*0.6
        individual.append(budget)
    trajectories.append(individual)
x = np.array(trajectories)
for i in range(0,1000):
    if x[i][999]>=1:
        plt.plot(range(0,1000),x[i], color="red", linewidth=1)
for i in range(0,1000):
    if x[i][999]<1:
        plt.plot(range(0,1000),x[i], color="gray", linewidth=.05)

plt.yscale('log')
plt.xlabel("Number of Iterations")
plt.ylabel("Earnings (Log Scale)")
plt.title("Individual Trajectories of Budget Sized Gambles")
plt.show()

trajectories = []
for examples in range(0,1000):
    bet = 1
    budget = 1
    individual = [1]
    for steps in range(1,1000):
        if random.randint(0,1)==1:
            budget += bet*1.5
        else:
            budget += -bet*0.6
        individual.append(budget)
    trajectories.append(individual)
x = np.array(trajectories)
for i in range(0,1000):
    if x[i][999]<1:
        plt.plot(range(0,1000),x[i], color="gray")
for i in range(0,1000):
    if x[i][999]>=1:
        plt.plot(range(0,1000),x[i], color="red", linewidth=.02)
plt.yscale('linear')
plt.xlabel("Number of Iterations")
plt.ylabel("Earnings")
plt.title("Individual Trajectories of Fixed Size Gambles")
plt.show()